|
|
|
Close Help | ||||||||||||||
III. MATHEMATICAL FRAMEWORK FOR LEARNING AUTOMATA
Recognizing the need for the formal presentation of a learning model, in this chapter we present a detailed review to the mathematics of the various existing LA models that relate to the hypothesized HCLSA model presented in the next chapter. We provide a unified nomenclature in order to develop the concepts in a straightforward manner.
Appendices A and B provide a brief, but complete, overview of the probability and stochastic automata concepts required to understand the material presented in this chapter. Equations numbered with an A or a B refer to these appendices, respectively.
In the field of sequential machines and automata, various authors have suggested several models for learning, always maintaining a strong mathematical flavor in their publications; yet, as we mentioned earlier, mathematical analysis is possible only for systems of limited complexity. AI scientists consider the analysis of complexity of capital importance. We have accepted the following trade-off. First, simple models are introduced at a low level which permits mathematical formality using stochastic automata theory; then, a rather elaborate computer simulation is used to test the hypotheses of a hierarchical model, representing a higher level of complexity.
III. 1 Deterministic Automata (DA)
The use of sequential machines for learning was initially introduced in 1961 by the Russian mathematician M. Tsetlin (57). At the time, he was concerned with the implementation of a deterministic automaton (DA) interacting with a random environment, that would represent the mathematical models of learning used in the discipline of psychology, such as t maze experiments. Today, applications have achieved a higher level of complexity with the inclusion of stochastic models.
Being deterministic, Tsetlin's DA is simple in principle; however, in order to obtain a good performance, it requires a large number of internal states.Before giving a formal definition of the model, let us describe the interaction between an automaton and a binary random environment (BRE), working as an evaluator, in the feedback fashion presented in Figure III. 1.
In the figure, x is a binary evaluation produced by the environment at time t, corresponding to the action y, selected at time t by the automaton. The mapping function, as conceived by Tsetlin, is a random variable X (t) that takes a value from the binary set {0,1} where 1 stands for a penalty (meaning that the output Y(t)=y, selected by the automaton, was erroneous), and 0 for a non-penalty.
The probability of selection 0 or 1 is given is given by a vector R (Response). It contains as many elements as outputs of the automaton exist (i.e., ymax). The element ry of R contains the probability of a penalty (i.e., X(t)=1) when the output given by the automaton was y. The BRE mechanism is represented by the selection at the y entry y of the vector R. (See Figure III.2)
Although it would be possible to represent the automaton as a Mealy machine, it is rather convenient to associate an output y for a given state. Therefore, we shall represent this automaton as a Moore machine that accepts an input X(t), moves to state Q(t+1) and delivers an output Y (t+1) as a function of the state.
An intuitive thought leads us to believe that the best automaton is the one which is penalized the least; this is correct (58). However, in order to have more comprehensive evaluation of the performance of the automaton, we present the measurements expediency and optimality, as defined below. These measurements are the basis for evaluating the performance of any learning automaton.
Assuming the behavior of the environment to be stationary and knowing that the penalty probabilities are given by R, we note that if the automaton behaved in a purely random manner, the amount of punishment received in the long run would be given by:

If the penalty satisfies the condition of being the expected value
given in (1), then the automaton is said to be expedient. In this
way, expediency compares the behavior of a Deterministic Automaton versus
a Stochastic Automaton. It is fair to say that not all proposed stochastic
models may compare favorably with deterministic ones.
On the other hand, looking at R, we realize that the smallest amount
of punishment is obtained when the automaton selects the output y that
corresponds to the entry r min where ![]()
An automaton for which the penalty received is eventually and exclusively equal to r min without limit, then it is said to behave asymptotically optimal.
Tsetlin provided a linear scheme to synthesize an asymptotically optimal automaton. For the case of a 2 state machine, his results are similar to those reported by Robbins (see Fu 19) in a related problem in t maze experiments, generally known as the two armed bandit problem. The problem is so named because the automaton must predict which gun a bandit is going to draw.
To formulate the problem, let us define the interaction between a deterministic automaton and a binary random environment as the pair I= (DA, BRE), where the DA is given by the quintuple:Interactions with binary random environments whose output set is 0 or 1 and are known as P (Penalty) models. When the environment selects its output from a discrete set of elements, we refer to the interaction as Q (Quantized) models, see Fu (19). Finally, when the outputs are taken from a closed continuous interval, the interaction is considered as S (Strength) model, see Narendra & Thathachar (37). Appendix B presents the detailed solution of the interaction (BRE, DA). To determine the performance of such as interaction, we have only to compute the following values:
III.2. Learning Stochastic Automata (LSA)
Stochastic models are divided in two types, those with a fixed structure (SAFS), and those with a variable structure (SAVS). In this section we discuss a SAFS using as an example the model developed by Krilov (see 58) and then go into the more interesting LSA models with variable structure.
III.2.1. Stochastic Automata with Fixed Structure (SAFS).
The SAFS automaton, as proposed by Krilov, is similar to the DA previously discussed, with the difference that the P (1) matrix is stochastic; i.e., there is possible choice on the next state for the case of a penalty input, X (t) = 1. The probabilities in P (1) remain constant in time and so the matrix is stationary and ergodic, presenting a steady-state solution. It is then relatively simple to determine the expected values to test expediency and optimality. For the case of non-penalty input, the automaton remains deterministicThe strategy for a SAFS for the two-armed bandit problem denoted by K2n,2 is expressed by the following heurism:
In any penalty driven transition give a 50% chance of selecting the stage suggested for a penalty input in the L2n,2 strategy, and 50% chance for the state suggested in the non-penalty input case in the same strategy. Otherwise behave as a regular L2n,2 automaton.The heurism can be represented, for X (t) = 1, by the diagram presented in Figure III.4. It can be shown (see Appendix B) that the performance of a K2,2 is also expedient. Krilov's approach, although generating the same expected value, is worth mentioning since it represents the first application of stochastic automata to learning.
III.2.2. Stochastic Automata with Variable Structure (SAVS)
In 1963, Varshavsky and Vorontsova (65) published a paper suggesting the use of a compensation algorithm to modify the transition matrix of a stochastic automaton according to the outcome given by the environment after every single transition matrix of a stochastic automaton according to the outcome given by the environment after every single transition.
The idea has been described vaguely by Michie (32), although his work is oriented to game playing.

A SAVS is defined as the sextuple:

As stated earlier, the algorithm is called algedonic loop, see Beer (7). The word comes from the Greek "algos": pain; "edos": pleasure. In learning automata theories, it is generally referred to as reward/punishment reinforcement schemes.
The interaction between the environment and the automaton in a SAVS is rather important, since it affects the whole structure of the matrix, transition. In this way, the stochastic matrices P ( ) are not homogeneous any longer. However, provided that the environment remains stationary, there are some algedonic schemes that allow for the mathematical solution of the interaction through the use of nonhomogeneous markov chains.
The steady state solution for the values of II, denoted by tpij(y), is assumed when any of the following conditions hold true:
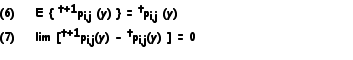
The first condition is the solution of the martingale equation. Since we only make the expectation at time t+1 equal to the value at some time t, we cannot assure that the final values will be the same. Therefore, some measurement for stability is required. The second condition tells us that as t approaches infinity, the matrices get saturated and the interactions can be described by homogeneous chains from then on.
The solution of two examples, proposed originally by Varshavsky and Varontsova, is presented in Appendix B. The compensation or reinforcement algorithm used is given by the following linear algedonic scheme:

The analytical solution of these schemes leads us to the following expected value, showing expedient behavior.
E {{SAVS, BRE}} = 2r1r0 / (r0+r1)
An important aspect to consider here is the fact that although the behavior is the same as that of the previous models, the strategy was not embedded in the initial structure; it was learned after the conditioning to which the automaton was exposed. Learning, as we defined it, takes place in an LSA. ø is an important parameter since its value affects the rate of convergence. Several simulations must be carried out in order to obtain the fastest learning time.
A non-linear scheme for this SAVS is given by incrementing tpij(x) according to the following algorithm:

With the application of NLAS, it has been shown (58) that the SAVS behaves asymptotically optimal when ro < 1 /2 < r1 ; i.e., E{{SAVS, BRE }} = rmin = ro.When both r 1 < 1/2, and ro < 1/2, then it has also been shown in (58) that the expected value
E{{ SAVS, BRE}}= lim E{{L2n,n, BRE}}
Therefore, two state automata generate as good results as a DA with infinite number of states, provided that the SAVS be given enough time to learn the strategy. One way in which these examples can be generalized is by simply maintaining stochasticity in the various matrices P. For the case of a non-penalty input, once the probability of the chosen transition is increased, the normalization of the rest of the entries in the row generally takes place in one of two possible ways: either they are equally decreased to compensate for the increase, or each is decreased by an amount proportional to its current value. For the case of a penalty input, the procedure is similar, with the difference that the chosen probability is reduced and this decrement is spread over the entire row.
Using the following proportional normalization, the author has obtained adequate results for a game playing program (22):

A simple modification to this algedonic algorithm suggest using (1- ø ) instead ø of for the case of a penalty, to compensate differently for a reward than for a penalty.In any case, the value for ø must be < 1. Algorithm (10) can be modified to spread the value uniformly, ie. indpendent of pik(x) , as follows:

In this case we must keep track of the current value of tpij (x) when updating a given row. The non-linear scheme described by (9) can now be generalized for n states and n + 1 order, as follows:

We present now two definitions based on the work of Narendra and Thathachar (37); a SAVS is said to be e optimal if:
![]()
The definition simple states that for cases where asymptotic optimality cannot be obtained, it is desirable to set a tolerance e > 0 that stops the compensation. A SAVS is said to be absolutely expedient if
![]()
Where the notation t E{}represents the expected value obtained in the t iteration. The definition implies that the penalty received by the automaton is monotonically decreasing.

So far we have only encountered binary environments; the generalization of the interactions of learning automata with other environments is also described in the literature. Fu (19) presents the interaction of the S model, i.e., the environment may evaluate with a normalized continuous value between 0 and 1. Such an interaction is graphically depicted in Figure III.5. In the figure, x e [ 0, 1] and A is the corresponding algedonic compensation scheme used for updating the matrices. As we observe, the SAVS consists of two elements: the stochastic memory that selects the output Y(t), and the compensation evaluator that determines the compensation to be applied to the SAVS, on the basis of the input x(t). For the compensation, Fu proposes the following general form :
![]()
In this case, the equation holds for all possible transitions and tLik(x) is a function that depends on both the input x and the chosen transition i --> k. The equation has a solution in the limit, obtainable provided the L function is time independent for such case it becomes:
![]()
With the limit solution
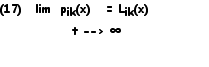
In general, we define a function tI(xmin) as an index of performance that the evaluator computes given the input x; such index is used to obtain the values for n ik(x) necessary for the compensation. A simple form for I is defined as follow:
![]()
In this way, the value of t I(x) is normalized for the range of values and the various n values are given by:
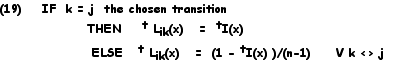
We can now define the algedonic compensation for this model as follows:

When Ith is a threshold value, the previous scheme becomes similar to that given by (10). In his work, Fu (19), showed that this linear scheme is absolutely expedient.We note that in the generalization of both P and S models, the stochastic matrices can be made autonomous, i.e., input independent. For example, in the cases shown for the SAVS, the steady state solution for both P (1) and P (0) are the same, generating a resulting matrix with equal entries as those of the P's. For the sake of simplicity in the notation, when dealing with these interactions, we will refer only to a single P matrix, shortening the p (x) notation to just p. Although in the case of single stochastic automata some authors have gone one step further and have reduced the stochastic matrices into single vectors with a unique initial state, due to our interest in collective automata, we find it convenient to keep the matrix notation.
Later work by Narendra & Thathachar (37), Chandresekaran (13) and
other has greatly simplified the concepts of LA. The main concern of these
authors lies on the definition of convergence theorems and other measurements
of performance to determine the best algedonic schemes. For the case of
S models, Narendra and Viswanathan (38) present a set of compensations
that exhibit optimality. The following algedonic scheme represents their
Reward-Inaction method:
The previous scheme is called reward-inaction due to the fact that the matrix P is only updated when a non-penalty input is received from the environment.

The interaction in this case is defined by the pair I = {SAVS, NRE} where the SAVS is similar to that given in (5), but with P being single input-independent and A being the algedonic scheme for S models. The normalized random environment is therefore defined as:

Since in any SAVS we have a set of non-homogeneous matrices we can no longer talk about a steady-state solution. Let us defined t ßy as:

In the work of Chandresekaran and Shen (13) as well as in Viswanathan (66) the derivations of convergence theorems to test expediency are given for various schemes; these theories derived from the solution of the equations presented in (6) and (7) when presented as martingale equations as follows:
![]()
The solution of the equation is in general rather difficult, though for the case of two or three states, the solution is straightforward. In any case, it is necessary to test for the stability of each of the roots.The concept of stability in LA has been debated and criticized. However, it is an adequate test for optimality in an analytical tractable fashion. Thathachar and Laskmivaran (29) provide a single theorem to unify the results for absolute expediency. An algedonic compensation scheme is said to be absolutely expedient if, and only if, the following two general equations hold:
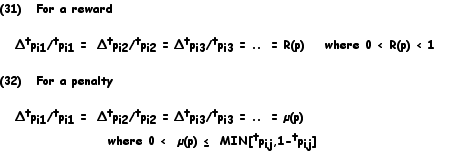
A corollary of the theorem is as follows: The compensations should vary on time and should depend on the probability values of the transitions. For example, while scheme PLAS (10) may be absolutely expedient, scheme ULAS (11), is not.
For the e optimality, little is known about a method to analytically determine the adequacy of a scheme and, in any case, the mathematical derivations are very complex. An interesting point reported by Narendra & Thathachar (37) is that all the schemes which exhibited optimality in their work , also exhibited absolutely expedient behavior.
III.2.3. Simulation of Single LSA's
The schemes and examples reported in the literature that allow for mathematical solution are only limited and therefore much of the research relies on simulation studies. Narendra and Viswanathan (38) reported the use of the following computed metrics to determine the advantage of some schemes:
For a P Model with a unique starting state:

The important findings already reported are that the performance of optimal schemes is far better than the absolutely expedient ones. Secondly, reward-inaction schemes generate optimality. The study of single stochastic automata in a Q model is covered in the section on collective automata
III. 3 Collective Learning Stochastic Automata (CLSA)
Working with a set of automata instead of a single automaton to perform a learning task, is an idea that has already been described in the literature. We may classify this approach in three distinct categories; hierarchical, parallel and sequential.A hierarchical arrangement of two automata was proposed by Viswanathan (66) to accommodate the complexity of a non-stationary random environment. Since we devote Chapter IV to the discussion of hierarchical models, we are postponing the description of such an arrangement.
Parallel models have been widely used for the solution of n-person games. We distinguish two types of games, namely, competitive and cooperative. Competitive games can be further subdivided into games played against a random player, and those played between two LSA's. In the first case, the game is denoted by the pair {LSA, BRE}, similar to the interactions previously described. In the second case, the two automata play against each other and the interaction is denoted y the triple {LSA1, LSA2, RC}, where both LSA's are of the types already described and RC is the referee of the game. The graphical representation of two LA's in a competitive mode is presented in Figure III.6. The referee provides the algedonic information to each automaton in accordance with a pay-off table. In this way compensation takes place. Each automaton uses this feedback from the RC to compensate its state transition space.
The simulation studies reported in the literature, as well as some mathematical derivations (Tsetlin (58), Narendra and Thathachar (37) ) show that in the case of a SAVS with expedient behavior playing against a random player, the SAVS may achieve optimal pay-off only under certain conditions. For the case of an optimal scheme, the SAVS achieves optimal pay-off unconditionally: such fact agrees with the discussion that optimal schemes are better than expedient ones. An interesting way to test compensation schemes, suggested by Viswanathan (66), consists of putting two different schemes each LSA to test the advantage of any of them. Cooperative games are the best example of a parallel model in collective automata. The model is defined to be a set of n LSA's interacting with a single environment simultaneously, and where the input x(t), produced by the environment is identical for all of them. This output delivered by the environment is a function of the outcome of all LSA's involved and therefore, the selection of the next state by each automaton is rewarded provided that it contributes to a mutual benefit. There are various modifications to this arrangement, e.g., allowing each automata to use a different compensation scheme allowing all automata to have the same state table, etc.
Since our main interest in this research lies in sequential models, we shall not devote more time to parallel models. Greater detail is presented in the work of Varshavsky (53).
III. 3.1. Sequential Collection of Automata
The idea of a sequential collection of automata for learning can e found in the work of Michie (32) as early as 1961. The learning machine discussed for a game of tic-tac-toe represents a clear example of an ad-hoc model of a CLSA. The term CLSA, and to a great extent the motivation for this research, appeared for the first time in a paper by Bock (8). In his work, he covers the topic of stochastic learning in a rather different manner than any previous LA author. The example is a guessing game, e.g., a numerical code-breaking, presenting the results based on simulation studies. The discussion is certainly less formal due to the mathematical intractability of the nonhomogeneous Markov chains he deals with. An important simplification stated is the assumption of a deterministic environment. A diagram of Bock's CLSA is shown in Figure III.8 The model seems more human-like since the performance of the automaton is only measured after a given number of transitions have taken place, i.e., until a final state is reached. Based upon the transitions taken to the final state. i.e., the solution path, the environment deterministically delivers a single composite evaluation to the automaton.
After a review of the panorama of LA both conceptually and mathematically, we now turn to the core of this research, namely: the formalization of the CLSA; a discussion of new algedonic schemes; the presentation of the HCLSA; and its simulation studies.
III.3.2. Formalization of a CLSA
In order to describe Bock's CLSA in terms of the notation used in this study, we define the interaction of the automaton based on a Q model. The interaction is notated by the pair (CLSA, QDE) where the CLSA is defined by the sextuple:

Since the function e considers both Y and T as independent variables, it may be defined in various ways. For example, the value of e may be determined by the number of incorrect outputs delivered by the CLSA. Better still, since g is a one-to-one function of the state e may determine the number of incorrect state transitions taken. In fact, this is the definition used by Bock. Furthermore, X(t) can be defined as a measure of closeness to a given goal. This is implemented by considering only the last element in T, i.e., t (nmax).

In order to define expediency and optimality for the interaction, we must obtain the expected amount of penalty delivered by the environment to a random automaton. Let us consider the case of e defined as the number of incorrectly chosen outputs. Assuming that the starting state Q (t) is known, we have that:
![]()
To obtain P{X(t+nmax)=i}, let us analyze the probability of each outcome.
The probability of choosing a correct state is given by the inverse of
the number of states, i.e., 1/qmax. Choosing an incorrect state is obviously
1-1/qmax. Since the nmax transitions are independent and considering all
possible combinations, we have:![]()
Where: x is the count of incorrect states and nmax = qmax-1 since the initial state is assumed to be known in advance. The probability of equation (40) has a binomial distribution with parameter (1-1/qmax) where the expected value is given by:
![]()
While the solution of the interaction of a single LSA with a deterministic environment is rather trivial (e.g., via an efficient search algorithm in T), this is not so for the CLSA because the environment delivers a summarial evaluation only after nmax transitions. The amount of penalty for the interaction {CLSA, QDE} is defined as:
![]()
Expedient behavior is said to exist provided that: E{{CLSA,QDE}} < E{QDE}. Furthermore, it will be absolute expediency if equation (42) increases monotonically as n decreases. When dealing with a deterministic environment, optimal behavior is obtained when Y = T, i.e., no penalty is generated. This may be difficult to obtain and we must be contented with optimality. (See (37)). Optimality and optimality exist if the expected values of the interaction is zero and less than respectively, as n becomes large. The general solution of equation (42) is analytically intractable for n>3 depending on the compensation policy used. It is convenient to use the steady-state concepts defined by equations (6) and (7) and test the scheme by means of computer simulations. This is the method discussed in Bock's paper.The compensation used in that paper is a modified reward inaction linear scheme (MRIAS), that may be presented as follows:

The specification of the stationary compensation function c(x) is important in the behavior of the automata. Several forms were tested; an exponential form in suggested based on good empirical results. The specific value of ø is also important; Bock reports that ø= 0.25 gave the best results. The stationary compensation,ø , is constant throughout the process. With this limitation the automata may fail to reach optimality due to the fact that as error x decreases, all probabilities are rewarded more heavily. Intuitively, while an error of 3 at the beginning of the process might indicate improvement, implying that the path should be rewarded, after a large number of interactions, such a large error ought to be considered as a failure. To solve the problem, Bock suggests the use of a non-stationary compensation function ø* = f(ø ,t) that remains stationary for all transitions, i.e., nmax, but that changes in the next interaction.
In a more recent work, R. Plourde (49), working with Bock, tested the hypothesis of a non-stationary compensation algorithm. In his model, two variations of compensation are investigated, interstage and intrastage compensation. The concept of interstage compensation uses function that depends on the stage of learning. In this way, compensation at the beginning of a learning session is different from compensation at a later time. Intrastate compensation is also used in his model, since each transition is compensated on the basis of the specific location in the vector. Y where it appears. for this part, he uses a search algorithm to find the best values for this aspect of the compensation. Using generally the same algorithms as that given by procedure (43), R. Plourde modified C(x) in order to consider the aspects of interstage and intrastage compensation.

He concluded that e optimality is found for e > 0.073. We consider it important to state that this was obtained with thousands of runs. The rationale of this approach can be understood if we consider the previously defined error function as a measure of nearness to a goal state; it is then assumed that the initial transitions of a given interaction should not be rewarded as much as the final ones, e.g., nmax, nmax-1, nmax-2, due to the fact that they do not contribute as much to the final goal.
A final point on Bock,s paper: he uses the entropy of the state transition matrix as a measure of performance. According on Bock's paper: he uses the entropy of the state transition matrix as a measure of performance. According to Shannon (see Ashby (3)), entropy is given by:
![]()
The value of entropy S is a maximum when all the transition probabilities for a given row i are the same, e.g., the contents of the matrix P at the beginning of the first interaction, before any compensation takes place. Bock suggests that it would appear useful (though not sufficient) to try to minimize S so that only one tpij has a value for every row, thus saturating the matrix to follow a single path. However, it may be that a low entropy path is an erroneous one. Entropy should be used with care since it can only serve as a measure of intensity of learning.Interestingly enough, Bock uses it to test the CLSA capacity to "unlearn" or neutralize a learned path. This is done by reversing the compensation policy an maximizing S.
III.3.3. Variations on the Compensation Schemes
In an attempt to emulate human behavior, and to look for better performance in a CLSA Templeman (5.5) measures the expectation of the penalty X(t) for a given selected output vector Y(t). In a program to learn a board game, he allows the automaton to compute an RMS expectation polynomial for the penalty. Such polynomial predicts the goodness of the vector Y selected, and its coefficients are updated as learning takes place.
Once the real penalty is delivered by the environment, the algedonic scheme compares the expected penalty with the value actually obtained. If the penalty (or reward) received is similar to the expected, little compensation takes place. On the other hand, if the CLSA expects a small amount of penalty, and the environment delivers a high value, then the automaton makes large modifications of probabilities of the transitions taken. Expanding Templeman's concept, we give an overall additive algedonic scheme that covers some of the intuitive factors that should affect a compensation. These factors are:

In this scheme, M represents the mean value of the probability of the path taken by the automaton, i.e., the expected probability of a correct answer. Modifications to the scheme can also use a mean of the normalized entropy S of the chosen path. Following the ideas of Templeman for expected errors, function V server as a measure of the parameter x and x, i.e., error and differential error. This function can be represented as a look-up table (see Figure III.8). The entries to the table are the values of x and x and the output of the table is a value for a given amount of reward or penalty to be given to the automaton. In the figure, the upper left-hand corner contains the best V values, since it represents both a minimum error x with a minimum increase in the error; as a matter of fact, the increase negative.On the other end, the lower right-hand corner keeps the worst case values, since it represents the highest error x and the highest increase in the error. The linear approach presented in the figure is for the set of {0,1,2,3} for the values of x. In this case, the analytical solution to the function is:
![]()
In general, one may define any desired mapping. In any case, the values of the function must be normalized if the transition matrix P is to remain stochastic. However, such normalization may decrease the relevance of the function V.